数据结构与算法-图
《学习JavaScript数据结构与算法(第3版)》
图是网络结构的抽象模型。图是一组由边连接的节点(或顶点)。任何二元关系都可以用图来表示。
一个图(G)由一组顶点(V)和一组连接顶点的边(E)组成。G=(V, E)
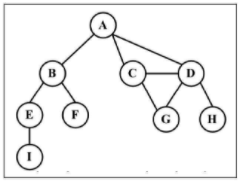
相邻顶点:由一条边连接在一起的顶点。
度:一个顶点的度是其相邻顶点的数量。
路径:路径是顶点v1, v2,…, vk的一个连续序列,其中vi和vi+1是相邻的。
简单路径要求不包含重复的顶点。环也是一个简单路径。
如果图中不存在环,则称该图是无环的。如果图中每两个顶点间都存在路径,则该图是连通的。
图可以是无向的(边没有方向)或是有向的(有向图)。
如果图中每两个顶点间在双向上都存在路径,则该图是强连通的。
图还可以是未加权的或是加权的。
图的表示
从数据结构的角度来说,我们有多种方式来表示图。在所有的表示法中,不存在绝对正确的方式。图的正确表示法取决于待解决的问题和图的类型。
邻接矩阵(最常见)
每个节点都和一个整数相关联,该整数将作为数组的索引。用一个二维数组来表示顶点之间的连接。如果索引为 i 的节点和索引为 j 的节点相邻,则 array[i][j] === 1,否则 array[i][j] === 0,如下图所示。
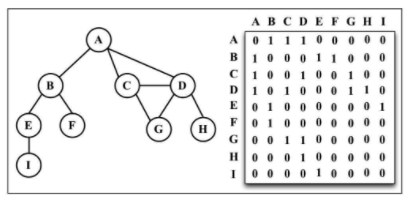
不是强连通的图(稀疏图)如果用邻接矩阵来表示,则矩阵中将会有很多0,这意味着我们浪费了计算机存储空间来表示根本不存在的边。例如,找给定顶点的相邻顶点,即使该顶点只有一个相邻顶点,我们也不得不迭代一整行。邻接矩阵表示法不够好的另一个理由是,图中顶点的数量可能会改变,而二维数组不太灵活。
邻接表
邻接表由图中每个顶点的相邻顶点列表所组成。可以用数组、链表、散列表或字典来表示相邻顶点列表。
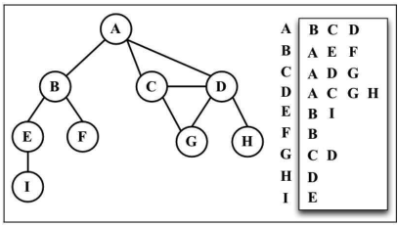
关联矩阵
在关联矩阵种,矩阵的行表示顶点,列表示边。使用二维数组来表示两者之间的连通性,如果顶点 v 是边 e 的入射点,则array[v][e] === 1;否则,array[v][e]=== 0。
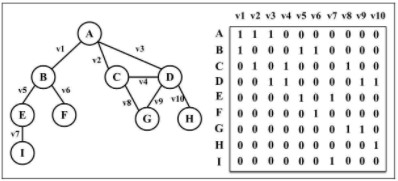
关联矩阵通常用于边的数量比顶点多的情况,以节省空间和内存。
图的数据结构
使用邻接表的表示方式进行构造。
class Graph {
construct(isDirected = false) {
this.isDirected = isDircted; // 表示图是否有向,默认情况下,图是无向的
this.vertices = []; // 数组来存储图中所有顶点的名字
this.adjList = new Dirctionary(); // 使用字典来存储邻接表,字典将会使用顶点的名字作为键,临界顶点列表作为值
}
// 添加新的顶点
addVertex(v) {
if (!this.vertices.includes(v)) { // 判断待插入顶点是否不存在于图中
this.vertices.push(v); // 将顶点添加到顶点列表中
this.adjList.set(v, []); // 在邻接表中,设置顶点v作为键对应的字典值为一个空数组
}
}
// 添加顶点之间的边
addEdge(a, b) { // 接收两个要建立连接的顶点作为参数
if (!this.adjList.get(a)) { // 验证顶点是否存在于顶点数组中,如果不存在,则加入顶点数组中
this.addVertex(a);
}
if (!this.adjList.get(b)) { // 验证顶点是否存在于顶点数组中,如果不存在,则加入顶点数组中
this.addVertex(b);
}
this.adjList.get(a).push(b); // 添加一条自顶点a到顶点b的边
if (this.isDirected !== true) { // 如果是无向图
this.adjList.get(b).push(a); // 添加一条自顶点b到顶点a的边
}
}
// 返回顶点列表
getVertices() {
return this.vertices;
}
// 返回邻接表
getAdjList() {
return this.adjList;
}
// 输出图
toString() {
let s = '';
for (let i = 0; i < this.vertices.length; i++) { // 迭代顶点数组
s += `${this.vertices[i]} -> `; // 取得第一个顶点
const neighbors = this.adjList.get(this.vertices[i]); // 取得列表的邻接表
for (let j = 0; j < neighbors.length; j++) { // 迭代邻接表,输出相邻顶点
s += `${neighbors[j]} `;
}
s += '\n';
}
return s;
}
}图的遍历
算法:广度优先搜索(BFS)和深度优先搜索(DFS)
图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径,检查图是否连通,检查图是否含有环,等等。
图遍历算法的思想是必须追踪每个第一次访问的节点,并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法,都需要明确指出第一个被访问的顶点。
完全探索一个顶点要求查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点,将其标注未被发现的,并将其加进待访问顶点列表中。
为了保证算法的效率,务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到。
广度优先搜索和深度优先搜索的区别:
- 广度优先搜索采用的数据结构是队列,将顶点存入队列,最先入队的顶点先被探索。
- 深度优先搜索采用的数据结构是栈,将顶点存入栈,顶点是沿着路径被探索的,存在新的相邻顶点就去访问。
使用颜色来表示被访问状态:
- 白色:表示该顶点未被访问。
- 灰色:表示该顶点被访问过,未被探索过。
- 黑色:表示该顶点被访问过且被完全探索过。
const Colors = {
WHITE: 0,
GREY: 1,
BLACK: 2
};
// 初始化每个顶点的颜色
const initializeColor = vertices => {
const color = {};
for (let i = 0; i < vertices.length; i++) {
color[vertices[i]] = Colors.WHITE;
}
return color;
};广度优先搜索(BFS)
广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的邻点(相邻顶点),就像一次访问图的一层。
从顶点v开始的广度优先搜索算法所遵循的步骤:
- 创建一个队列
Q。 - 标注
v为被发现的(灰色),并将v入队列Q。 - 如果
Q非空,则运行以下步骤:- 将
u从Q中出队列; - 标注
u为被发现的(灰色); - 将
u所有未被访问过的邻点(白色)入队列; - 标注
u为已被探索的(黑色)。
- 将
// 广度优先搜索,接受图和第一个顶点作为参数,最后进行回调操作
export const breadthFirstSearch = (graph, startVertex, callback) => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices); // 初始化图的所有顶点
const queue = new Queue(); // 创建队列,用来存储待访问和待探索的顶点
queue.enqueue(startVertex); // 将起始点存入队列
while (!queue.isEmpty()) { // 如果队列非空
const u = queue.dequeue(); // 从队列中移除一个顶点u
const neighbors = adjList.get(u); // 获取顶点u的邻接表
color[u] = Colors.GREY; // 当前顶点u颜色设置为灰色
for (let i = 0; i < neighbors.length; i++) { // 循环取出顶点u的邻接点
const w = neighbors[i]; // 顶点u的邻接点赋值
if (color[w] === Colors.WHITE) { // 判断当前邻接点是否未被访问
// 未被访问过
color[w] = Colors.GREY; // 设置被访问状态
queue.enqueue(w); // 将邻接点加入队列中,当该点出队时,进行对该点探索
}
}
// 探索完该顶点和其邻接点后
color[u] = Colors.BLACK; // 设置顶点u为已探索状态
if (callback) { // 如果有回调函数
callback(u); // 回调函数处理当前探索顶点
}
}
};使用广度搜索算法寻找最短路径
给定一个图G和源顶点v,找出每个顶点u和v之间最短路径的距离(以边的数量计)。
- 从v到u的距离*distance[u]*;
- 前溯点predecessors[u],用来推导出从v到其他每个顶点u的最短路径。
// 广度搜索寻找最短路径
export const BFS = (graph, startVertex) => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
const queue = new Queue();
const distances = {}; // 表示距离
const predecessors = {}; // 表示前溯点
queue.enqueue(startVertex);
// 迭代每个顶点,用来初始化距离和前溯点
for (let i = 0; i < vertices.length; i++) {
distances[vertices[i]] = 0;
predecessors[vertices[i]] = null;
}
// 迭代队列中的顶点,直到队列为空
while (!queue.isEmpty()) {
const u = queue.dequeue();
const neighbors = adjList.get(u);
color[u] = Colors.GREY;
for (let i = 0; i < neighbors.length; i++) {
const w = neighbors[i];
if (color[w] === Colors.WHITE) {
color[w] = Colors.GREY;
distances[w] = distances[u] + 1; // 距离+1
predecessors[w] = u; // 设置w的前溯点u
queue.enqueue(w);
}
}
color[u] = Colors.BLACK;
}
return { // 最后返回距离和前溯点对象
distances,
predecessors
};
};通过前溯点数组,可以用下面代码来构建从顶点A到其他顶点的路径
const fromVertex = myVertices[0]; // 源顶点A
for (let i = 1; i < myVertices.length; i++) { // 循环所有顶点
// 对于除A顶点外的其他顶点,计算其到顶点A的距离
const toVertex = myVertices[i];
const path = new Stack(); // 创建路径栈
// 追溯toVertex到fromVertex的路径,变量v被赋值为前溯点值,进行反向追溯路径
for (let v = toVertex; v !== fromVertex; v = shortestPathA.predecessors[v]) {
path.push(v);
}
path.push(fromVertex); // 将源顶点推入路径栈中
let s = path.pop(); // 创建路径字符串,并赋值路径第一个字符串
while (!path.isEmpty()) { // 路径栈为非空,则拼接路径
s += ' - ' + path.pop();
}
console.log(s); // 输出路径
}深度优先搜索(DFS)
深度优先搜索算法将会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后一个顶点被访问,接着原路回退并探索下一条路径。即先深度后广度地访问顶点。
深度优先搜索算法不需要一个源顶点。在深度优先搜索算法中,若图中顶点v未访问,则访问该顶点v。
要访问顶点v,照如下步骤做:
- 标注v为被发现的(灰色);
- 对于v的所有未访问(白色)的邻点w,访问顶点w;
- 标注v为已被探索的(黑色)。
// 接收图和回调函数作为参数
export const depthFirstSearch = (graph, callback) => {
const vertices = graph.getVertices(); // 图的顶点
const adjList = graph.getAdjList(); // 图的邻接表
const color = initializeColor(vertices);
for (let i = 0; i < vertices.length; i++) { // 迭代顶点
if (color[vertices[i]] === Colors.WHITE) { // 未被访问过的顶点
depthFirstSearchVisit(vertices[i], color, adjList, callback);
}
}
};
// 递归函数
const depthFirstSearchVisit = (u, color, adjList, callback) => {
color[u] = Colors.GREY; // 修改当前顶点颜色状态
if (callback) { // 如果有回调函数进行回调
callback(u);
}
const neighbors = adjList.get(u); // 邻接表中找到顶点u的所有邻接点
for (let i = 0; i < neighbors.length; i++) { // 遍历邻接点列表
const w = neighbors[i];
if (color[w] === Colors.WHITE) { // 如果邻接点未被访问过
// 继续向下递归,邻接点都按深度访问了之后回退
depthFirstSearchVisit(w, color, adjList, callback);
}
}
// 设置当前点已被探索状态
color[u] = Colors.BLACK;
};改进深度优先算法
对于给定的图G,深度优先搜索算法将遍历图G的所有节点,构建“森林”(有根树的一个集合)以及一组源顶点(根),并输出两个数组:发现时间和完成探索时间。可以修改depthFirstSearch函数来返回一些信息:
- 顶点u的发现时间*d[u]*;
- 当顶点u被标注为黑色时,u的完成探索时间*f[u]*;
- 顶点u的前溯点*p[u]*。
export const DFS = graph => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
const d = {};
const f = {};
const p = {};
const time = { count: 0 }; // 用来追踪发现时间和完成探索时间
for (let i = 0; i < vertices.length; i++) { // 迭代顶点,进行初始化
f[vertices[i]] = 0;
d[vertices[i]] = 0;
p[vertices[i]] = null;
}
for (let i = 0; i < vertices.length; i++) { // 迭代顶点
if (color[vertices[i]] === Colors.WHITE) { // 如果顶点第一次被发现
DFSVisit(vertices[i], color, d, f, p, time, adjList);
}
}
return {
discovery: d,
finished: f,
predecessors: p
};
};
const DFSVisit = (u, color, d, f, p, time, adjList) => {
color[u] = Colors.GREY; // 修改顶点被访问的状态
d[u] = ++time.count; // 追踪被发现时间
const neighbors = adjList.get(u); // 获取该点的邻接点
for (let i = 0; i < neighbors.length; i++) { // 遍历邻接点
const w = neighbors[i];
if (color[w] === Colors.WHITE) { // 如果当前邻接点是未被访问过
p[w] = u; // 记录邻接点的前溯点
DFSVisit(w, color, d, f, p, time, adjList); // 进行递归探索邻接点
}
}
color[u] = Colors.BLACK; // 当前顶点修改为已探索状态
f[u] = ++time.count; // 记录探索完时间
};边是从最近发现的顶点u处被向外探索的。只有连接到未发现的顶点的边被探索了。当u所有的边都被探索了,该算法回退到u被发现的地方去探索其他的边。这个过程持续到发现了所有从原始顶点能够触及的顶点。如果还留有任何其他未被发现的顶点,对新源顶点重复这个过程。重复该算法,直到图中所有的顶点都被探索了。
使用深度优先搜索进行拓扑排序。
给定下图(有向无环图-DAG),假定每个顶点都是一个我们需要去执行的任务。
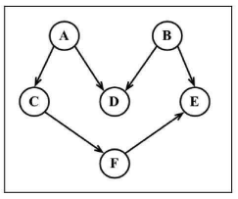
拓扑排序:编排一些任务或步骤的执行顺序。拓扑排序只能应用于有向无环图(DAG)。
const graph = new Graph(true); // 有向图
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F'];
for (let i = 0; i < myVertices.length; i++) {
graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('B', 'D');
graph.addEdge('B', 'E');
graph.addEdge('C', 'F');
graph.addEdge('F', 'E');
const result = DFS(graph);
const fTimes = result.finished;
let s = '';
for (let count = 0; count < myVertices.length; count++) {
let max = 0;
let maxName = null;
for (let i = 0; i < myVertices.length; i++) {
if (fTimes[myVertices[i]] > max) {
max = fTimes[myVertices[i]];
maxName = myVertices[i];
}
}
s += ' - ' + maxName;
delete fTimes[maxName];
}
console.log(s);拓扑排序结果有多种可能性。
最短路径算法
Dijkstra算法
Dijkstra算法是一种计算从单个源到所有其他源的最短路径的贪心算法,即可以用来计算从图的一个顶点到其余各顶点的最短路径。
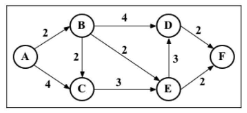
// 邻接矩阵表示图
const graph = [[0, 2, 4, 0, 0, 0],
[0, 0, 1, 4, 2, 0],
[0, 0, 0, 0, 3, 0],
[0, 0, 0, 0, 0, 2],
[0, 0, 0, 3, 0, 2],
[0, 0, 0, 0, 0, 0]];Dijkstra算法:
const INF = Number.MAX_SAFE_INTEGER; // 安全数最大整数
// 选出距离最近的顶点,搜索dist数组中的最小值,返回它在数组中的索引
const minDistance = (dist, visited) => {
let min = INF;
let minIndex = -1;
for (let v = 0; v < dist.length; v++) {
if (visited[v] === false && dist[v] <= min) {
min = dist[v];
minIndex = v;
}
}
return minIndex;
};
const dijkstra = (graph, src) => {
const dist = [];
const visited = [];
const length = graph.length;
for (let i = 0; i < length; i++) { // 遍历初始化
dist[i] = INF; // 把所有距离(dist)初始化为无限大
visited[i] = false;
}
dist[src] = 0; // 把源顶点到自己的距离设为0
for (let i = 0; i < length - 1; i++) { // 找出到其他顶点的最短距离
const u = minDistance(dist, visited); // 选出距离最近的顶点
visited[u] = true; // 把选出的顶点标为visited, 以面重复计算
for (let v = 0; v < length; v++) {
// 如果找到更短的路径
if (!visited[v] && graph[u][v] !== 0 &&
dist[u] !== INF && dist[u] + graph[u][v] < dist[v]) {
// 更新最短路径的值
dist[v] = dist[u] + graph[u][v];
}
}
}
return dist; // 处理完所有顶点后,返回从源顶点(src)到图中其他顶点最短路径的结果
};Floyd-Warshall算法
Floyd-Warshall算法是一种计算图中所有最短路径的动态规划算法。通过该算法,可以找出从所有源到所有顶点的最短路径。
export const floydWarshall = graph => {
const dist = [];
const { length } = graph;
// 把dist数组初始化为每个顶点之间的权值
for (let i = 0; i < length; i++) {
dist[i] = [];
for (let j = 0; j < length; j++) {
if (i === j) {
dist[i][j] = 0; // 顶点到自身的距离为0
} else if (!isFinite(graph[i][j])) { // 如果两个顶点之间没有边,则表示为Infinity
dist[i][j] = Infinity;
} else {
dist[i][j] = graph[i][j]; // i到j可能的最短距离就是顶点间的权值
}
}
}
// 将顶点0到k作为中间点,从i到j的最短路径经过k
for (let k = 0; k < length; k++) {
for (let i = 0; i < length; i++) {
for (let j = 0; j < length; j++) {
// 计算通过顶点k的i和j之间的最短路径
if (dist[i][k] + dist[k][j] < dist[i][j]) {
// 如果最短路径比已知最短路径小,则更新最短路径
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
return dist; // 输出
};最小生成树(MST)
最小生成树(MST)问题是网络设计中常见的问题。也可应用于岛桥问题。
如要在n个岛屿之间建造桥梁,如何用最低的成本实现所有岛屿相连互通。
Prim算法
Prim算法是一种求解加权无向连通图的MST问题的贪心算法。它能找出一个边的子集,使得其构成的树包含图中所有顶点,且边的权值之和最小。
const INF = Number.MAX_SAFE_INTEGER;
// 选出距离最短(权值最小)的顶点
const minKey = (graph, key, visited) => {
let min = INF;
let minIndex = 0;
for (let v = 0; v < graph.length; v++) {
if (visited[v] === false && key[v] < min) {
min = key[v];
minIndex = v;
}
}
return minIndex;
};
export const prim = graph => {
const parent = [];
const key = [];
const visited = [];
const { length } = graph;
for (let i = 0; i < length; i++) { // 把所有顶点key初始化为无限大
key[i] = INF;
visited[i] = false;
}
key[0] = 0; // 第一个key作为第一个顶点
parent[0] = -1; // 第一个顶点总是MST的根节点
// 对所有顶点求MST
for (let i = 0; i < length - 1; i++) {
const u = minKey(graph, key, visited);
visited[u] = true; // 将选出的顶点visited状态改为true
for (let v = 0; v < length; v++) {
// 如果发现更小的权值
if (graph[u][v] && !visited[v] && graph[u][v] < key[v]) {
// 保存MST路径并更新其权值
parent[v] = u;
key[v] = graph[u][v];
}
}
}
return parent;
};Kruskal算法
Kruskal算法也是一种求加权无向连通图的MST的贪心算法。
const INF = Number.MAX_SAFE_INTEGER;
//
const find = (i, parent) => {
while (parent[i]) {
i = parent[i]; // eslint-disable-line prefer-destructuring
}
return i;
};
const union = (i, j, parent) => {
if (i !== j) {
parent[j] = i;
return true;
}
return false;
};
// 初始化邻接矩阵
const initializeCost = graph => {
const cost = [];
const { length } = graph;
for (let i = 0; i < length; i++) {
cost[i] = [];
for (let j = 0; j < length; j++) {
if (graph[i][j] === 0) {
cost[i][j] = INF;
} else {
cost[i][j] = graph[i][j];
}
}
}
return cost;
};
export const kruskal = graph => {
const { length } = graph;
const parent = [];
let ne = 0;
let a;
let b;
let u;
let v;
const cost = initializeCost(graph); // 初始化邻接矩阵
while (ne < length - 1) { // 当MST的边数小于顶点总数减1时
// 找出权值最小的边
for (let i = 0, min = INF; i < length; i++) {
for (let j = 0; j < length; j++) {
if (cost[i][j] < min) {
min = cost[i][j];
a = u = i;
b = v = j;
}
}
}
// 检查MST中是否已存在这条边,以避免环路。
u = find(u, parent);
v = find(v, parent);
// 如果u和v是不同的边,则将其加入MST
if (union(u, v, parent)) {
ne++;
}
cost[a][b] = cost[b][a] = INF; // 从列表中移除这些边,以免重复计算
}
// 返回MST
return parent;
};