数据结构与算法-算法设计
《学习JavaScript数据结构与算法(第3版)》
分而治之
分而治之是算法设计中的一种方法。它将一个问题分成多个和原问题相似的小问题,递归解决小问题,再将解决方式合并以解决原来的问题。
分而治之算法可以分成三个部分。
- 分解原问题为多个子问题(原问题的多个小实例)。
- 解决子问题,用返回解决子问题的方式的递归算法。递归算法的基本情形可以用来解决子问题。
- 组合这些子问题的解决方式,得到原问题的解。
动态规划
动态规划(dynamic programming, DP)是一种将复杂问题分解成更小的子问题来解决的优化技术。
注意,动态规划和分而治之是不同的方法。分而治之方法是把问题分解成相互独立的子问题,然后组合它们的答案,而动态规划则是将问题分解成相互依赖的子问题。
用动态规划解决问题时,要遵循三个重要步骤:
- 定义子问题;
- 实现要反复执行来解决子问题的部分(递归);
- 识别并求解出基线条件。
应用问题:
- 背包问题:给出一组项,各自有值和容量,目标是找出总值最大的项的集合。这个问题的限制是,总容量必须小于等于“背包”的容量。
- 最长公共子序列:找出一组序列的最长公共子序列(可由另一序列删除元素但不改变余下元素的顺序而得到)。
- 矩阵链相乘:给出一系列矩阵,目标是找到这些矩阵相乘的最高效办法(计算次数尽可能少)。相乘运算不会进行,解决方案是找到这些矩阵各自相乘的顺序。
- 硬币找零:给出面额为d1, …, dn的一定数量的硬币和要找零的钱数,找出有多少种找零的方法。
- 图的全源最短路径:对所有顶点对*(u, v),找出从顶点u到顶点v*的最短路径。
最少硬币找零问题
最少硬币找零问题是硬币找零问题的一个变种。硬币找零问题是给出要找零的钱数,以及可用的硬币面额d1,…, dn及其数量,找出有多少种找零方法。最少硬币找零问题是给出要找零的钱数,以及可用的硬币面额d1,…, dn及其数量,找到所需的最少的硬币个数。
例如:有面值1美分,5美分,10美分,25美分的硬币,如果要找36美分的零钱,如何找到所需最小硬币数。
// coins代表硬币面额 amount表示总零钱
function minCoinChange(coins, amount) {
const cache = []; // 更加高效,不重复计算值
const makeChange = (value) => { // 递归函数
if (!value) { // value为0 则返回空数组 基线条件
return [];
}
if (cache[value]) { // 检查结果缓存,如果有,则直接返回结果 基线条件
return cache[value];
}
let min = []; // 找零硬币面额
let newMin;
let newAmount;
// 遍历硬币面额,对每个面额都计算剩余价值
for (let i = 0; i < coins.length; i++) {
const coin = coins[i]; // 当前硬币面额
newAmount = value - coin; // 一直减少,直到找到最小钱数
if (newAmount >= 0) {
// 进入递归
newMin = makeChange(newAmount); // 计算找零结果
}
// newAmount是否有效,minValue最少硬币数是否最优解,minValue和newAmount是否是合理的值
if (
newAmount >= 0 &&
(newMin.length < min.length - 1 || !min.length) &&
(newMin.length || !newAmount)
) {
// 则表示当前解为最优解
min = [coin].concat(newMin);
}
}
// 返回最少硬币结果
return (cache[value] = min);
};
// 调用递归函数
return makeChange(amount);
}背包问题(0-1背包)
背包问题是一个组合优化问题。它可以描述如下:给定一个固定大小、能够携重量W的背包,以及一组有价值和重量的物品,找出一个最佳解决方案,使得装入背包的物品总重量不超过W,且总价值最大。
这项从顶部开始构建解决方案的技术被称为记忆化,而解决方案就在表格或矩阵的右下角。
如题,背包总重量只有5,如何装可以使总价值最大?

// 找到解决方案
function findValues(n, capacity, kS) {
let i = n;
let k = capacity;
while (i > 0 && k > 0) { // 迭代二维数组
if (kS[i][k] !== kS[i - 1][k]) {
i--;
k -= kS[i][k];
} else {
i--;
}
}
}
// capacity背包容量,weights重量数组,values价值数组,n为物品总数
function knapSack(capacity, weights, values, n) {
const kS = []; // 结果矩阵
for (let i = 0; i <= n; i++) { // 初始化寻找方案的二维矩阵
kS[i] = [];
}
for (let i = 0; i <= n; i++) {
for (let w = 0; w <= capacity; w++) { // 背包容量迭代
// 只处理索引不为0的列和行,并且迭代数组中每个可用的项
if (i === 0 || w === 0) {
kS[i][w] = 0;
} else if (weights[i - 1] <= w) { // 物品i的重量小于当前背包容量,背包装得下
// 计算当前背包价值
const a = values[i - 1] + kS[i - 1][w - weights[i - 1]];
// 不含当前物品的最优子集为上一个物品的当前背包容量的价值
const b = kS[i - 1][w];
kS[i][w] = a > b ? a : b; // max(a,b)
} else {
// 当前物品大于背包容量,背包装不下,则当前最大价值是上一个物品的最优子集
kS[i][w] = kS[i - 1][w];
}
}
}
findValues(n, capacity, kS);
return kS[n][capacity];
}
// --------------------------------------------------
// 递归版本
function knapSack(capacity, weights, values, n) {
if (n === 0 || capacity === 0) {
return 0;
}
if (weights[n - 1] > capacity) {
return knapSack(capacity, weights, values, n - 1);
}
const a = values[n - 1] + knapSack(capacity - weights[n - 1], weights, values, n - 1);
const b = knapSack(capacity, weights, values, n - 1);
return a > b ? a : b;
}最长公共子序列(LCS)
找出两个字符串序列的最长子序列的长度。最长子序列是指,在两个字符串序列中以相同顺序出现,但不要求连续(非字符串子串)的字符串序列。
function lcs(wordX, wordY) {
const m = wordX.length;
const n = wordY.length;
const l = [];
for (let i = 0; i <= m; i++) {
l[i] = [];
for (let j = 0; j <= n; j++) {
l[i][j] = 0;
}
}
for (let i = 0; i <= m; i++) {
for (let j = 0; j <= n; j++) {
if (i === 0 || j === 0) {
l[i][j] = 0;
} else if (wordX[i - 1] === wordY[j - 1]) {
l[i][j] = l[i - 1][j - 1] + 1;
} else {
const a = l[i - 1][j];
const b = l[i][j - 1];
l[i][j] = a > b ? a : b; // max(a,b)
}
}
}
return l[m][n];
}
// --------------------------------------
// 输出算法结果
function printSolution(solution, wordX, m, n) {
let a = m;
let b = n;
let x = solution[a][b];
let answer = '';
while (x !== '0') {
if (solution[a][b] === 'diagonal') {
answer = wordX[a - 1] + answer;
a--;
b--;
} else if (solution[a][b] === 'left') {
b--;
} else if (solution[a][b] === 'top') {
a--;
}
x = solution[a][b];
}
return answer;
}
function lcs(wordX, wordY) {
const m = wordX.length;
const n = wordY.length;
const l = [];
const solution = [];
for (let i = 0; i <= m; i++) {
l[i] = [];
solution[i] = [];
for (let j = 0; j <= n; j++) {
l[i][j] = 0;
solution[i][j] = '0';
}
}
for (let i = 0; i <= m; i++) {
for (let j = 0; j <= n; j++) {
if (i === 0 || j === 0) {
l[i][j] = 0;
} else if (wordX[i - 1] === wordY[j - 1]) {
l[i][j] = l[i - 1][j - 1] + 1;
solution[i][j] = 'diagonal';
} else {
const a = l[i - 1][j];
const b = l[i][j - 1];
l[i][j] = a > b ? a : b; // max(a,b)
solution[i][j] = l[i][j] === l[i - 1][j] ? 'top' : 'left';
}
}
}
return printSolution(solution, wordX, m, n);
}
矩阵链相乘
找出一组矩阵相乘的最佳方式(顺序)。
n行m列的矩阵A和m行p列的矩阵B相乘,结果是n行p列的矩阵C。相乘的顺序不一样,要进行的乘法运算总数也有很大差异。那么,要如何构建一个算法,求出最少的乘法运算次数。
function printOptimalParenthesis(s, i, j) {
if (i === j) {
// console.log('A[' + i + ']');
} else {
// console.log('(');
printOptimalParenthesis(s, i, s[i][j]);
printOptimalParenthesis(s, s[i][j] + 1, j);
// console.log(')');
}
}
export function matrixChainOrder(p) {
const n = p.length;
const m = [];
const s = [];
for (let i = 1; i <= n; i++) {
m[i] = [];
m[i][i] = 0;
}
for (let i = 0; i <= n; i++) {
// to help printing the optimal solution
s[i] = []; // auxiliary
for (let j = 0; j <= n; j++) {
s[i][j] = 0;
}
}
for (let l = 2; l < n; l++) {
for (let i = 1; i <= (n - l) + 1; i++) {
const j = (i + l) - 1;
m[i][j] = Number.MAX_SAFE_INTEGER;
for (let k = i; k <= j - 1; k++) {
// q = cost/scalar multiplications
// 计算给定括号顺序的乘法运算次数,并将值保存在辅助矩阵m中
const q = m[i][k] + m[k + 1][j] + ((p[i - 1] * p[k]) * p[j]);
if (q < m[i][j]) {
m[i][j] = q;
s[i][j] = k; // s[i,j] = Second auxiliary table that stores k
}
}
}
}
// console.log(m);
// console.log(s);
printOptimalParenthesis(s, 1, n - 1);
return m[1][n - 1];
}面试题
贪心算法
贪心算法遵循一种近似解决问题的技术,期盼通过每个阶段的局部最优选择(当前最好的解),从而达到全局的最优(全局最优解)。
最少硬币找零问题
贪心算法,从最大面额的硬币开始,拿尽可能多当前面额的硬币找零。当无法再拿更多时,继续迭代,拿第二大面额的硬币,依次继续。
function minCoinChange(coins, amount) {
const change = [];
let total = 0;
for (let i = coins.length; i >= 0; i--) { // 迭代硬币面额
const coin = coins[i];
while (total + coin <= amount) { // 相加后的总值小于总金额,就继续迭代
change.push(coin);
total += coin;
}
}
return change;
}分数背包问题
在分数背包问题中,可以装入分数的物品。
function knapSack(capacity, weights, values) {
const n = values.length;
let load = 0;
let val = 0;
for (let i = 0; i < n && load < capacity; i++) {
if (weights[i] <= capacity - load) { // 如果物品可以完整地装入背包
val += values[i];
load += weights[i];
} else { // 如果物品不能完整地装入背包,则计算能够装入部分的比例
const r = (capacity - load) / weights[i];
val += r * values[i];
load += weights[i];
}
}
return val;
}最长公共子序列
function lcs(wordX, wordY, m = wordX.length, n = wordY.length) {
if (m === 0 || n === 0) {
return 0;
}
if (wordX[m - 1] === wordY[n - 1]) {
return 1 + lcs(wordX, wordY, m - 1, n - 1);
}
const a = lcs(wordX, wordY, m, n - 1);
const b = lcs(wordX, wordY, m - 1, n);
return a > b ? a : b;
}矩阵链相乘
function matrixChainOrder(p, i = 1, j = p.length - 1) {
if (i === j) {
return 0;
}
let min = Number.MAX_SAFE_INTEGER;
for (let k = i; k < j; k++) {
const count =
matrixChainOrder(p, i, k) + matrixChainOrder(p, k + 1, j) + ((p[i - 1] * p[k]) * p[j]);
if (count < min) {
min = count;
}
}
return min;
}回溯算法
回溯是一种渐进式寻找并构建问题解决方式的策略。我们从一个可能的动作开始并试着用这个动作解决问题。如果不能解决,就回溯并选择另一个动作直到将问题解决。根据这种行为,回溯算法会尝试所有可能的动作(如果更快找到了解决办法就尝试较少的次数)来解决问题。
迷宫老鼠问题
假设我们有一个大小为N × N的矩阵,矩阵的每个位置是一个方块。每个位置(或块)可以是空闲的(值为1)或是被阻挡的(值为0),如下图所示,其中S是起点,D是终点。
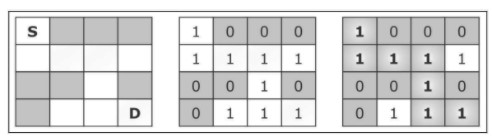
矩阵就是迷宫,“老鼠”的目标是从位置[0][0]开始并移动到[n-1][n-1](终点)。老鼠可以在垂直或水平方向上任何未被阻挡的位置间移动。
// 判断当前位置是否是空闲的
function isSafe(maze, x, y) {
const n = maze.length;
if (x >= 0 && y >= 0 && x < n && y < n && maze[x][y] !== 0) {
return true;
}
return false;
}
// 对于老鼠采取的每步行动,将路径标记为1。返回查找结果
// 递归函数
function findPath(maze, x, y, solution) {
const n = maze.length;
// 验证老鼠是否到达终点
if (x === n - 1 && y === n - 1) {
solution[x][y] = 1;
return true;
}
// 不是最后一步,验证老鼠能否安全移动到该位置
if (isSafe(maze, x, y) === true) {
solution[x][y] = 1; // 当前位置加入路径
// 水平向右移动到下一个位置
if (findPath(maze, x + 1, y, solution)) {
return true;
}
// 如果水平不可以,垂直向下移动到下一个位置
if (findPath(maze, x, y + 1, solution)) {
return true;
}
// 如果水平和垂直都不可以移动,则当前位置从路径中移除并回溯
solution[x][y] = 0;
return false;
}
return false;
}
function ratInAMaze(maze) {
const solution = [];
// 将每个位置初始化为0
for (let i = 0; i < maze.length; i++) {
solution[i] = [];
for (let j = 0; j < maze[i].length; j++) {
solution[i][j] = 0;
}
}
// 如果能够找到解,就返回矩阵
if (findPath(maze, 0, 0, solution) === true) {
return solution;
}
// 无解
return 'NO PATH FOUND';
}
数独解题器
目标是用数字1~9填满一个9×9的矩阵,要求每行和每列都由这九个数字构成。矩阵还包含了小方块(3×3矩阵),它们同样需要分别用这九个数字填满。谜题在开始给出一个已填了部分数字的矩阵,如下图所示。
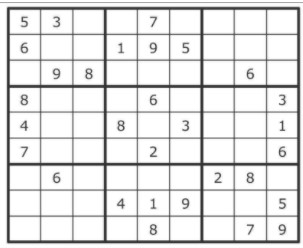
数独解题器的回溯算法会尝试在每行每列中填入每个数字。
const UNASSIGNED = 0;
// 判断数字在当前行是否出现过
function usedInRow(matrix, row, num) {
for (let col = 0; col < matrix.length; col++) {
if (matrix[row][col] === num) {
return true;
}
}
return false;
}
// 判断数字在当前列是否出现过
function usedInCol(matrix, col, num) {
for (let row = 0; row < matrix.length; row++) {
if (matrix[row][col] === num) {
return true;
}
}
return false;
}
// 判断数字在当前3*3矩阵是否出现过
function usedInBox(matrix, boxStartRow, boxStartCol, num) {
for (let row = 0; row < 3; row++) {
for (let col = 0; col < 3; col++) {
if (matrix[row + boxStartRow][col + boxStartCol] === num) {
return true;
}
}
}
return false;
}
// 检查数字是否符合规则
function isSafe(matrix, row, col, num) {
return (
!usedInRow(matrix, row, num) &&
!usedInCol(matrix, col, num) &&
!usedInBox(matrix, row - (row % 3), col - (col % 3), num)
);
}
function solveSudoku(matrix) {
let row = 0;
let col = 0;
let checkBlankSpaces = false;
// 验证数独问题是否被解决
for (row = 0; row < matrix.length; row++) {
for (col = 0; col < matrix[row].length; col++) {
if (matrix[row][col] === UNASSIGNED) {
// 有空白行 跳出循环
checkBlankSpaces = true;
break;
}
}
// 跳出两个循环
if (checkBlankSpaces === true) {
break;
}
}
// 表示问题已被完成
if (checkBlankSpaces === false) {
return true;
}
// 开始解题,尝试用1-9填写当前位置,进行迭代
for (let num = 1; num <= 9; num++) {
// 检查添加的数字是否符合规则
if (isSafe(matrix, row, col, num)) {
matrix[row][col] = num; // 填入数字
if (solveSudoku(matrix)) { // 递归进行填写下一个数字
return true;
}
// 如果不能填写下一个数字,则重新填写当前位置,进行回溯,填写下一个数字
matrix[row][col] = UNASSIGNED;
}
}
return false;
}
export function sudokuSolver(matrix) {
if (solveSudoku(matrix) === true) {
return matrix;
}
// 问题无解
return 'NO SOLUTION EXISTS!';
}